Drawing Fractals

Fractals are curious geometric shapes characterized by their recursive self-similarity, which means that a fractal will contain a fractal will contain a fractal will contain a fractal— StackOverflowError at line 3

Fractals are weird. They're essentially equations that have such an iconic graphical representation that an entire art form was built over them. The meandering shapes that repeat themselves infinitely, creating an oddly hypnotic or confusing display that is yet mathematically flawless. Certainly one of the more attractive products of mathematics. But seriously though, what even is a fractal?

To answer that question, I reached out to my most trustworthy friend: Wikipedia. According to it (and the four sources it cites) "a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension." Well. The first sentence was fine enough, but I'm afraid I'm not mathematician enough to understand what a "fractal dimension" or "topological dimension" is. The important fact here is that "many fractals appear similar at various scales. [...] This exhibition of similar patterns at increasingly smaller scales is called self-similarity". That's the important part: zoom in and you get the same thing again.

Ok, but... this only partly answers the question. Sure, now we know what the platonic ideal of a fractal is, but I'd like the actual mathematical description. Namely, I'd like to draw one. According to Wikipedia there's quite a few ways, and while they all seem pretty cool, the one that I'm going to focus on today is drawing fractals through L-systems.

Lindenmayer and turtles

A Lindenmayer system (or just L-system for short) is, in very basic layman's terms, a set of recursive instructions on how to construct a string from a known starting string. That... might seem a little weird at first. What do strings have to do with fractals? Isn't text a whole different beast compared to fractal geometry? Well, yes, that would be correct. However, the trick here is that the text in the string isn't the geometry itself, it's a set of instructions on how to draw.

See, in computer graphics there are a lot of ways to draw things on the screen. The pipeline from taking a bunch of binary bits and turning them into a colorful pixels is long and complicated, but we don't care about most of it. What we want is some way of drawing things on the screen so that we can make pretty little lines that make up a fractal. Since we only care about straight lines, we can use a rather fun method called turtle graphics.

Turtle graphics are a type of vector graphics where lines are traced by following a "cursor" object which leaves behind a "trail" when moving. Think of it like a little turtle walking over the canvas, leaving ink behind wherever it walks. This way, it draws its path and we get the final image. The way we control the creation of the image is by giving the turtle instructions on where to walk. Perhaps you see where I'm going with this. The L-system from before is a fancy way to create the list of instructions that we pass to the turtle to draw our fractal.

So say we acquired a turtle through undisclosed means. The turtle only takes two types of instructions: "walk forward" and "turn". We can tell it how far to walk and how much to turn, but that's about it. We'll have to make do with only those two instructions. As it turns out, that's actually all we need, at least for the fractals we'll be doing.

Let's do a quick overview of L-systems. Disclaimer: the extent of my understanding of L-systems is entirely limited to their Wikipedia page. I by no means claim to have any idea what I'm doing and claim no responsibility to any harm that befalls unto any turtle. With that out of the way, an L-system is made up of three pieces: an alphabet, an axiom and a set of production rules. They are a type of formal grammar, so if the terminology used here is reminiscent of linguistics, it's because it is linguistics, in a way.

• The alphabet is the set of characters we write with. Each character may be variable (it can be altered by a production rule; see below) or constant (it can't).
• The axiom is the string that we start with. It's kind of like a boundary condition for a differential equation. You just need a place to start and then the solution takes on from there. The solution is different for different starting conditions.
• Production rules are the meat and potatoes of the system. They are to L-systems what the time evolution operator is to the Schrödinger equation. You apply them to a state and they tell you what comes after. L-systems work in discrete steps, and at each step you apply all of the production rules. This is a big deal: if there is a production rule, it must be applied to all eligible cases, every step. This is how we can guarantee self-similarity: if a rule modifying a character creates more of that character, it will continue to recursively apply itself to its own output, causing perpetual self-cloning.

Algae

This may all sounds very abstract for now, so let's give an example to ground things. Lindenmayer was a botanist and originally created this formalism to describe the growth of plant matter^[1]. The growth of algae is particularly simple to describe. Let's see what our three components look like:

• Alphabet: A and B. Both variables.
• Axiom: A.
• Rules: A -> AB and B -> A.

Let's break this down. We are working with two characters here, A and B. What they represent really depends on what you're trying to accomplish. For this example, they're just symbols. We begin with the super simple string A, which is our "step 0". At each step, we apply the two production rules. Notice that A -> AB causes a positive feedback loop: the rule creates the same character it acts on, ensuring infinite cloning of the pattern. Let's write down the first few steps explicitly as an exercise:

0. A
1. AB
2. ABA
3. ABAAB
4. ABAABABA
5. ABAABABAABAAB

It goes on for as long as you like. These were made by applying the appropriate production rule on each character. I'm sure Lindenmayer got great use out this sequence, but for us it just acts as a good practical example of what we're about to do. I realize it might still look a bit... disconnected? But trust me, the only thing we need to add to make this make sense is an interpretation for A and B. Everything else will just fall into place.

The Koch snowflake

A good example to start from is the Koch snowflake. It's a line fractal that creates a shape that's very reminiscent of a snowflake, at least at higher iterations.

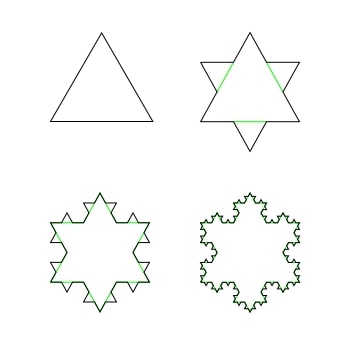
Image from the Koch snowflake Wikipedia page, original by user Wxs

It begins from an equilateral triangle (top left), each side of which gets modified to make add a little spike right in the center (top right). Rinse and repeat for each new side. As you can see, already by the third step (bottom right), it starts to look kind of like a snowflake. Let's try to describe it using an L-system.

Firstly, the alphabet. The basic idea is that each character symbolizes an instruction for the turtle. Since the turtle only understands two commands, we don't need that many symbols. To begin to understand what the turtle does, let's consider a single side, i.e. a line segment. We need to go from a straight segment to one with a small spike in it. The "spike" is really just a small equilateral triangle without the bottom side, so the angles of spike are all exactly 60 degrees. The spike also takes up exactly one third of the segment, right at the center. This is all the information we require. We only need to tell the turtle three things:

• Move forward. Call it →.
• Rotate by 60° clockwise. Call it ↻.
• Rotate by 60° counterclockwise. Call it ↺.

We now have our alphabet. The axiom is simple: to make a segment, we just need to go straight for the full length of the segment. In our alphabet, that's just →.

The production rules are the fun part. Luckily, there is only one Koch snowflake production rule. Each segment → must become that "spiked segment". To make a spiked segment, we can write →↺→↻↻→↺→. If this string looks like hieroglyphics, just try to imagine the turtle walking while it follows these commands. You'll see that it makes exactly the shape we want^[2].

To recap, our L-system is defined by:

• Alphabet: → (variable), ↻ and ↺ (constants^[3]).
• Axiom: →↻↻ →↻↻→ (an equilateral triangle).
• Rule: → becomes →↺→↻↻→↺→.

And that's it. We have encoded the entire fractal generation method into three lines of text. Now we just need to code it.

Interlude: The framework

Since we're going to use the same ideas for every fractal, we might as well define a central framework encoding the basic concepts. We're going to need to express the ideas of "point in space", "segment", "turtle" and "instructions".

Since we're using Julia, we'll be using a mix of structs and function methods defined for those structs. The common code can be found under common.jl. I won't go over every little detail here, but the code is commented. First, we'll define a 2D vector type and define basic vector algebra for it:

"""A 2-dimensional vector in Cartesian coordinates."""
mutable struct Point2{T <: AbstractFloat}
    x::T
    y::T
end

# 2D vector algebra
Base.:+(p1::Point2, p2::Point2) = Point2(p1.x + p2.x, p1.y + p2.y)
Base.:-(p::Point2) = Point2(-p.x, -p.y)
Base.:-(p1::Point2, p2::Point2) = Point2(p1.x - p2.x, p1.y - p2.y)
Base.:*(p::Point2, x::T) where {T <: Real} = Point2(p.x * x, p.y * x)
Base.:/(p::Point2, x::T) where {T <: Real} = Point2(p.x / x, p.y / x)
LinearAlgebra.norm(p::Point2) = p.x^2 + p.y^2

We'll use this for both points and direction vectors. If we wanted to be a bit fancier, it would be better to define a separate Vec2 type that is mutable and leave Point2 immutable as a reliable coordinate in space. For this code this is plenty enough, but for a library meant to be published it's something to consider. Let's also define a type to denote a segment in space:

"""A segment between two points."""
struct Segment{T <: AbstractFloat}
    start::Point2{T}
    finish::Point2{T} # end is a reserved keyword
end

function LinearAlgebra.norm(s::Segment)
    sqrt((s.finish.x - s.start.x)^2 + (s.finish.y - s.start.y)^2)
end

For convenience, let's also define types for open chains and polygons so that we can package our fractals into a single object. The only real difference is how the last vertex is treated:

"""
A chain made of an arbitrary number of sides. Unlike a `Polygon`, a `Chain` is not a closed shape and will not link the last and first vertex.
"""
struct Chain{T <: AbstractFloat}
    vertices::Vector{Point2{T}}
end

"""Create a `Chain` by concatenating multiple `Chain`s together."""
function Chain(chains::Vector{Chain})
    vertices = reduce(vcat, [c.vertices for c in chains])
    return Chain(vertices)
end

"""
A polygon made of an arbitrary number of sides. The last side is considered to be between the last and first vertex, so that it's a closed shape.
"""
struct Polygon{T <: AbstractFloat}
    vertices::Vector{Point2{T}}
end

"""Create a `Polygon` by concatenating multiple `Chain`s together."""
function Polygon(chains::Vector{Chain})
    vertices = reduce(vcat, [c.vertices for c in chains])
    # Since we are making a polygon from chains, it is assumed that the first and last
    # vertices will be the same, so we pop the last to one avoid duplicates
    pop!(vertices)
    return Polygon(vertices)
end

The turtle can be defined as a mutable object and the instructions as functions that mutate it:

"""The cursor for a basic turtle graphics implementation."""
mutable struct Turtle{T <: AbstractFloat}
    pos::Point2{T}
    dir::Point2{T}
end

"""
Moves the turtle forward by the given distance. Modifies in-place.
Returns the new position.
"""
function forward(turtle::Turtle, distance::T) where {T <: AbstractFloat}
    turtle.pos += turtle.dir * distance
end

"""
Rotate the turtle's walking direction by the given angle, counterclockwise. Modifies in-place.
Returns the new direction vector.
"""
function rotate(turtle::Turtle, angle::T) where {T <: AbstractFloat}
    # Rotation is a unitary operation so no need to renormalize dir
    new_x = turtle.dir.x * cos(angle) - turtle.dir.y * sin(angle)
    new_y = turtle.dir.x * sin(angle) + turtle.dir.y * cos(angle)
    turtle.dir.x = new_x
    turtle.dir.y = new_y
    return turtle.dir
end

Now for the engine. We need some function to encapsulate the idea of an L-system. It needs to take our axiom and our production rules and apply them back to back for $n$ steps, returning whatever comes out. This is a very general statement, so we can make a very general function:

"""
Draw the n-th iteration of a fractal by modifying each segment of the starting shape according to `segmenter`. `segmenter` must take a `Segment` as an argument and return a `Chain`.
The signature must look like `segmenter(s::Segment)::Chain`.
"""
function draw_fractal(
    shape::Polygon,
    segmenter::Function,
    iterations::Unsigned=1,
)::Polygon
    if iterations == 0
        return shape
    end

    # Each cycle takes the shape, breaks it down into edges, segments them and
    # reconstructs the new shape
    for _ in 1:iterations
        segs = segments(shape)
        curr_chains::Vector{Chain} = [segmenter(s) for s in segs]
        shape = Polygon(curr_chains)
    end

    return shape
end

(There's also another version with Chain instead of Polygon). The shape argument will be our axiom, whereas the segmenter function will be our production rule (we only need one). It is called this because it's purpose is to take a polygon edge and segment it into a more complicated shape, as determined by the production rule. iterations is the number of steps to run the L-system for.

And that's all. There's a few convenience function that I left out for brevity, but this is most of the code.

Drawing the snowflake

Now that we have the framework ready, we can use it to actually display something. Again, we need three things. An alphabet, an axiom and a set of production rules. The alphabet is taken care of by the forward and rotate functions for the Turtle object, so let's look at the other two.

The axiom is our starting shape. The Koch snowflake wants an equilateral triangle, so we'll give it just that:

A = Point2(0.0, 0.0)
B = Point2(0.5, sqrt(3) / 2)
C = Point2(1.0, 0.0)
triangle = Polygon([A, B, C])

As for the production rule, we need to define the segmenter function to pass to draw_fractal. It needs to take a Segment as an input and output a Chain. Here is where we get to use our turtle:

function koch_segmenter(seg::Segment, antiflake=false)::Chain
    spin = antiflake ? -1 : 1
    seg_length = norm(seg)
    direction = (seg.finish - seg.start) / seg_length
    step = seg_length / 3

    turtle = Turtle(seg.start, direction)

    # Production rule is → becomes →↺→↻↻→↺→
    A = seg.start
    B = forward(turtle, step)
    rotate(turtle, spin * π / 3)
    C = forward(turtle, step)
    rotate(turtle, spin * -2π / 3)
    D = forward(turtle, step)
    rotate(turtle, spin * π / 3)
    E = forward(turtle, step)

    return Chain([A, B, C, D, E])
end

I added a second argument to also make an antiflake, which is just the Koch snowflake with inverted angles. That's it! With our framework, that's all we need to make a (line) fractal to an arbitrary number of iterations. We just need some code to plot several iterations to see how it changes:

graphs = [plot(triangle)]
titles = ["Starting shape"]
for i in 1:5
    poly = draw_fractal(triangle, s -> koch_segmenter(s, false), i)
    push!(graphs, plot(poly))
    titles = [titles... "Iteration $i"]
end

l = @layout [a b; c d; e f]
plot(
    graphs...,
    title=titles,
    layout=l,
    size=(1000, 1500),
    legend=false,
    plot_title="Koch Snowflake",
)

This draws a fractal for every iteration between 1 and 5 and plots it. We then make a nice 3x2 layout to showcase them all.

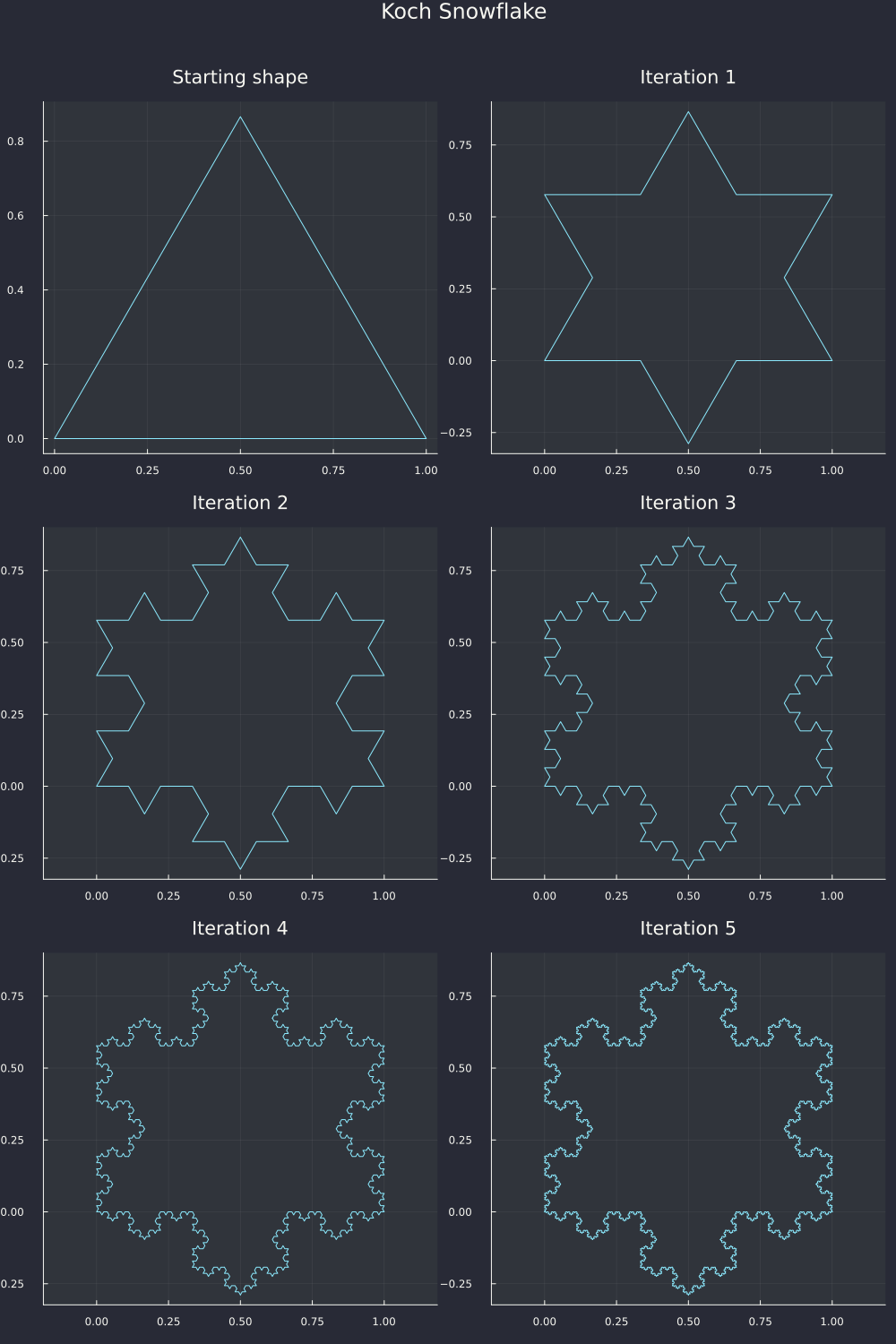
And it works! You can see how it becomes more and more complicated as the iterations go on, all due to a single rule that we set in the beginning. Isn't it pretty? You can totally make decorative patterns with this. No wonder fractal art is a thing. Let's also look at the antiflake.

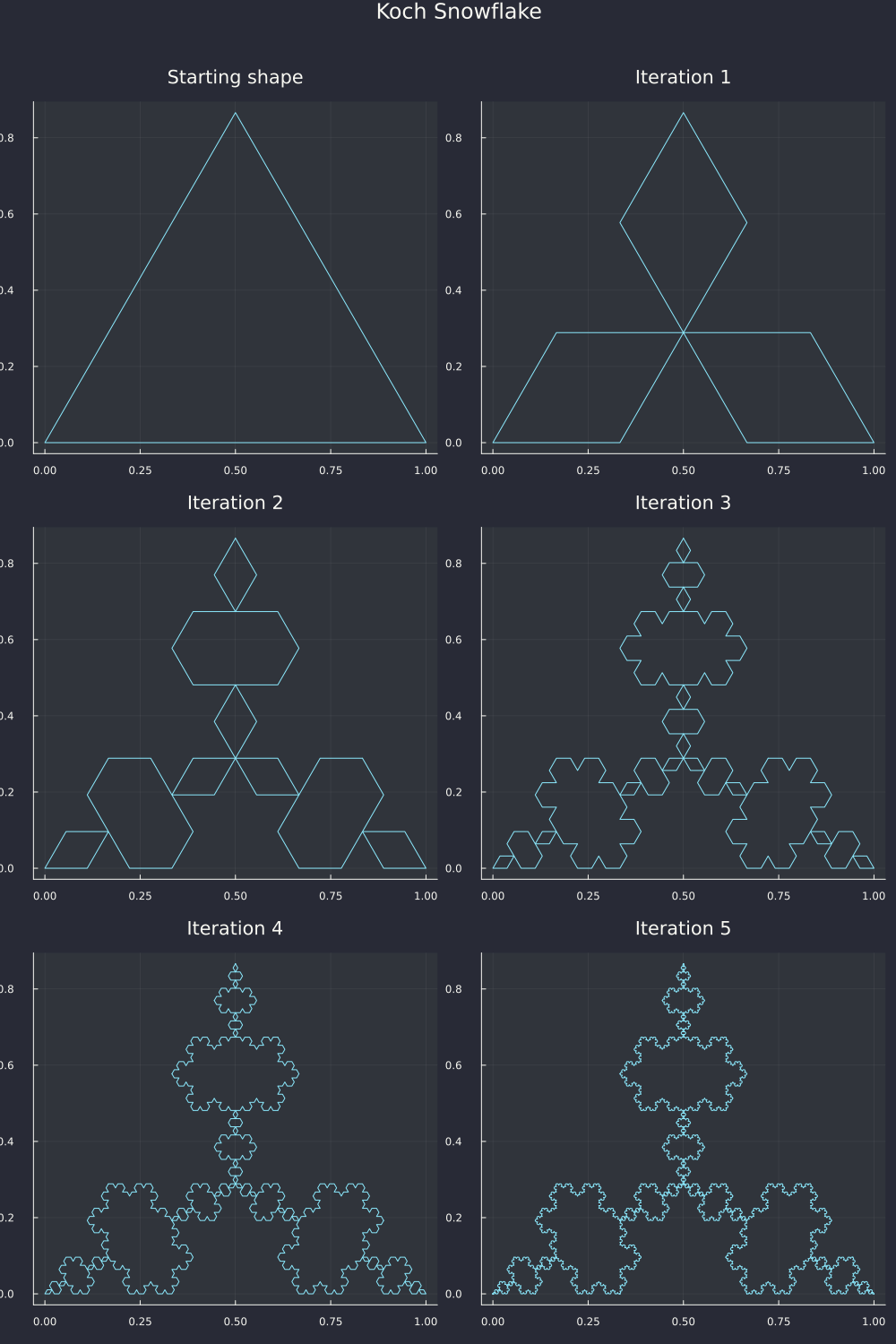
Well, would you look at that, we accidentally drew the Mitsubishi logo in iteration 1. The Wikipedia page doesn't mention anything about fractals, but it's a one-to-one match, so I'm fairly sure this is how they designed it too. Can't blame them, it's a clean design.

By the way, I did not get these right the first time. I inverted some indexes, messed up some vertices and I got a couple of... happy little accidents, let's call them.

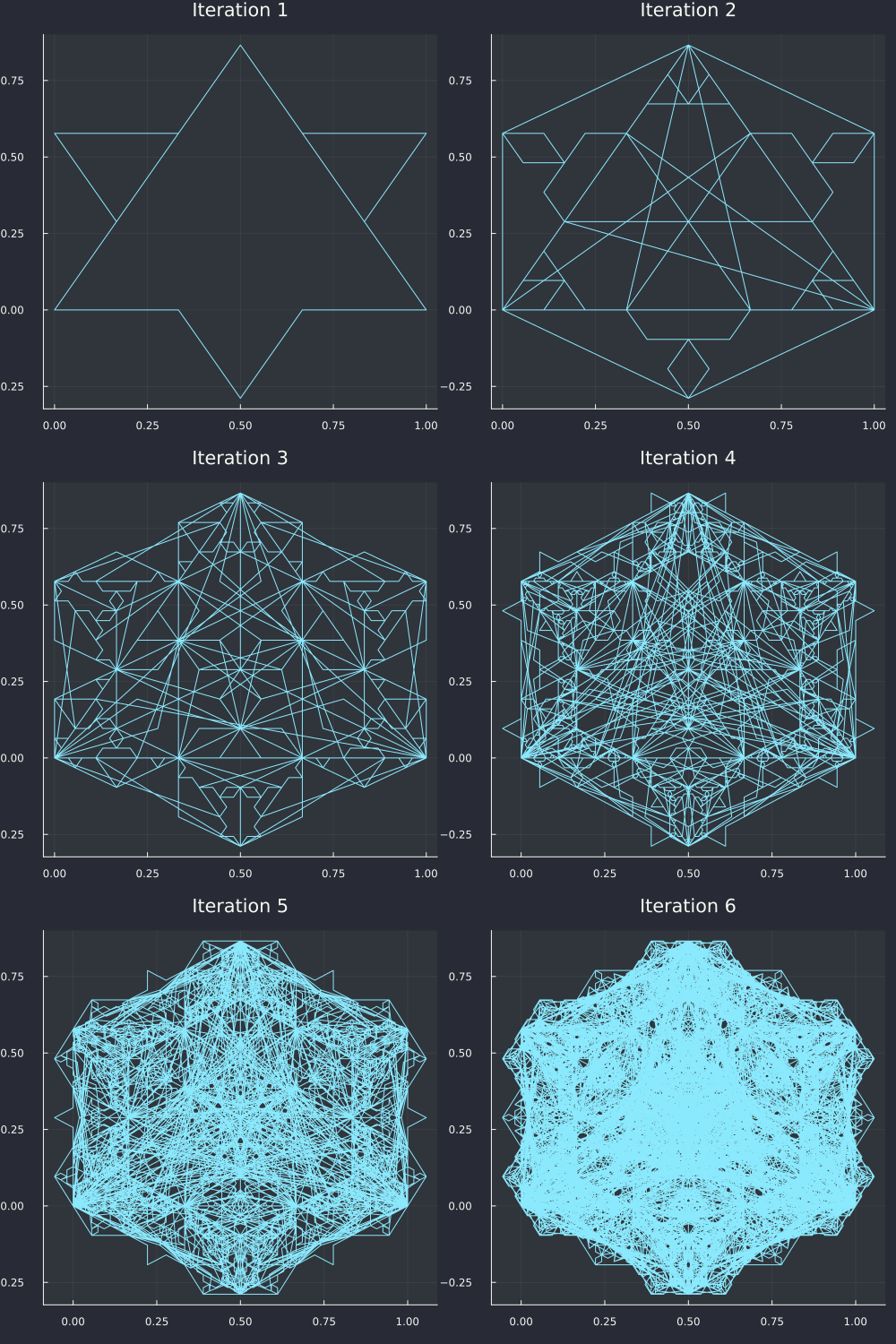
They still look kind of good in their own way, I think. You could put these in a sci-fi setting as some important symbol or logo and I'm sure people would like them.

Still, we made an entire framework to draw fractals, it would be such a waste to not make some more.

The Minkowski curve

Another straight-forward line fractal is the Minkowski curve, also known as the Minkowski sausage because it apparently vaguely resembles a sausage chain (I don't see it...). It's a line fractal that creates a very pretty-looking zig-zag pattern.

Image from the Minkowski sausage Wikipedia page, original by user Prokofiev

It begins from the simplest possible shape: a straight segment (1), which then gets modified to make a square-wave shape (2). Rinse and repeat. Let's try to describe it using an L-system:

• Alphabet: → (variable), ↻ and ↺ (constants, 90° degree rotations).
• Axiom: → (a line segment).
• Rule: → becomes →↺→↻→↻→→↺→↺→↻→.

A bit more complicated, but still manageable. Our segmenter function becomes

function minkowski_segmenter(seg::Segment)::Chain
    seg_length = norm(seg)
    direction = (seg.finish - seg.start) / seg_length
    step = seg_length / 4

    turtle = Turtle(seg.start, direction)

    # Production rule is → becomes →↺→↻→↻→→↺→↺→↻→
    A = seg.start
    B = forward(turtle, step)
    rotate(turtle, π / 2)
    C = forward(turtle, step)
    rotate(turtle, -π / 2)
    D = forward(turtle, step)
    rotate(turtle, -π / 2)
    E = forward(turtle, step)
    F = forward(turtle, step)
    rotate(turtle, π / 2)
    G = forward(turtle, step)
    rotate(turtle, π / 2)
    H = forward(turtle, step)
    rotate(turtle, -π / 2)
    I = forward(turtle, step)

    return Chain([A, B, C, D, E, F, G, H, I])
end

and with a starting axiom of

A = Point2(0.0, 0.0)
B = Point2(4.0, 0.0)
line = Chain([A, B])

we can reuse the same logic as before to make

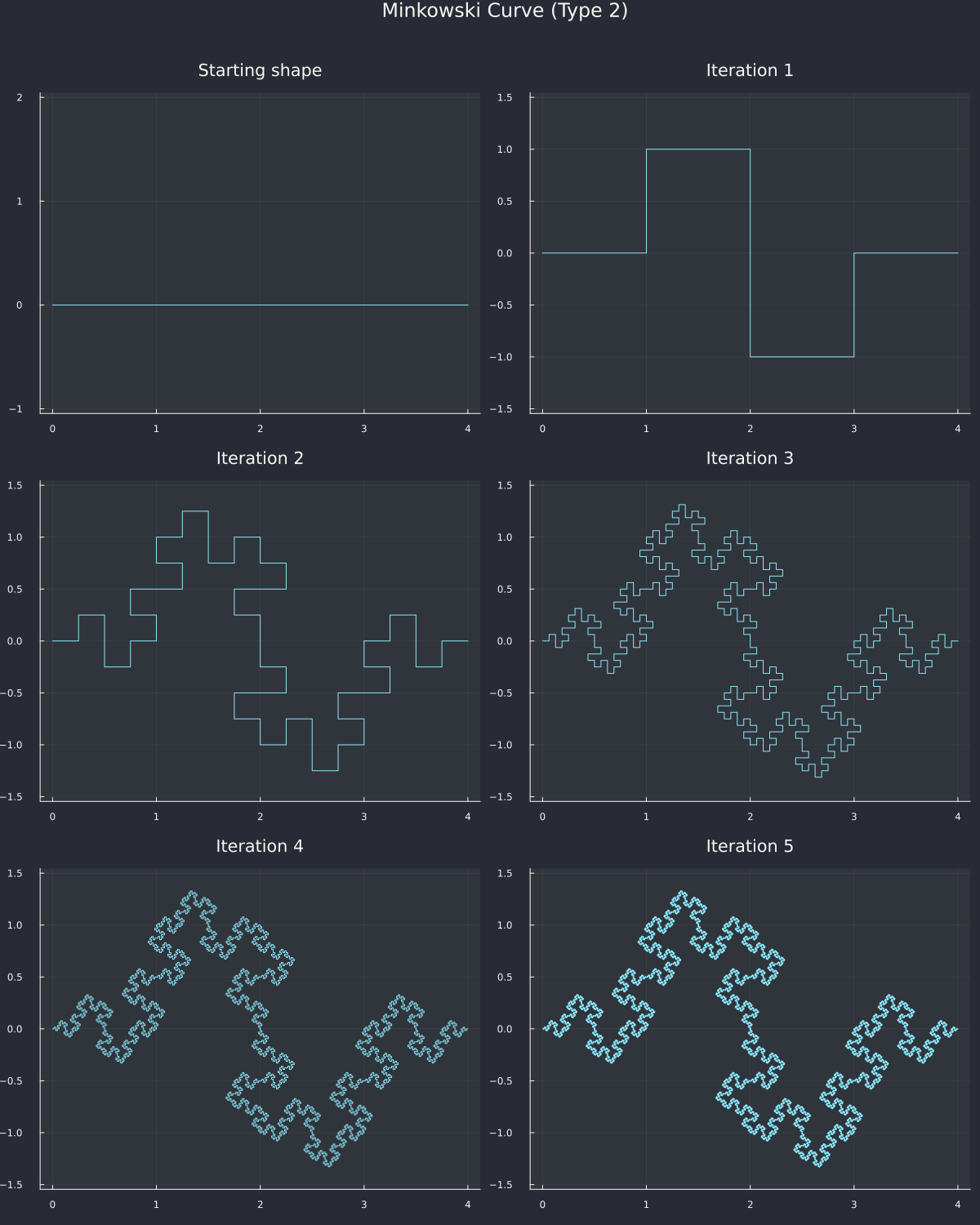
I like iteration 3 the most. You could put that on a Christmas sweater and it would be right at home (good luck telling grandma to knit that though). If you noticed the (Type 2) in the title, that's because there are two definitions for the Minkowski curve, and this is the second one. The first one is a bit further down. But first, for a fuller image, we can start from a box

A = Point2(0.0, 0.0)
B = Point2(4.0, 0.0)
C = Point2(4.0, 4.0)
D = Point2(0.0, 4.0)
box = Polygon([A, B, C, D])

to make a so-called Minkowski island:

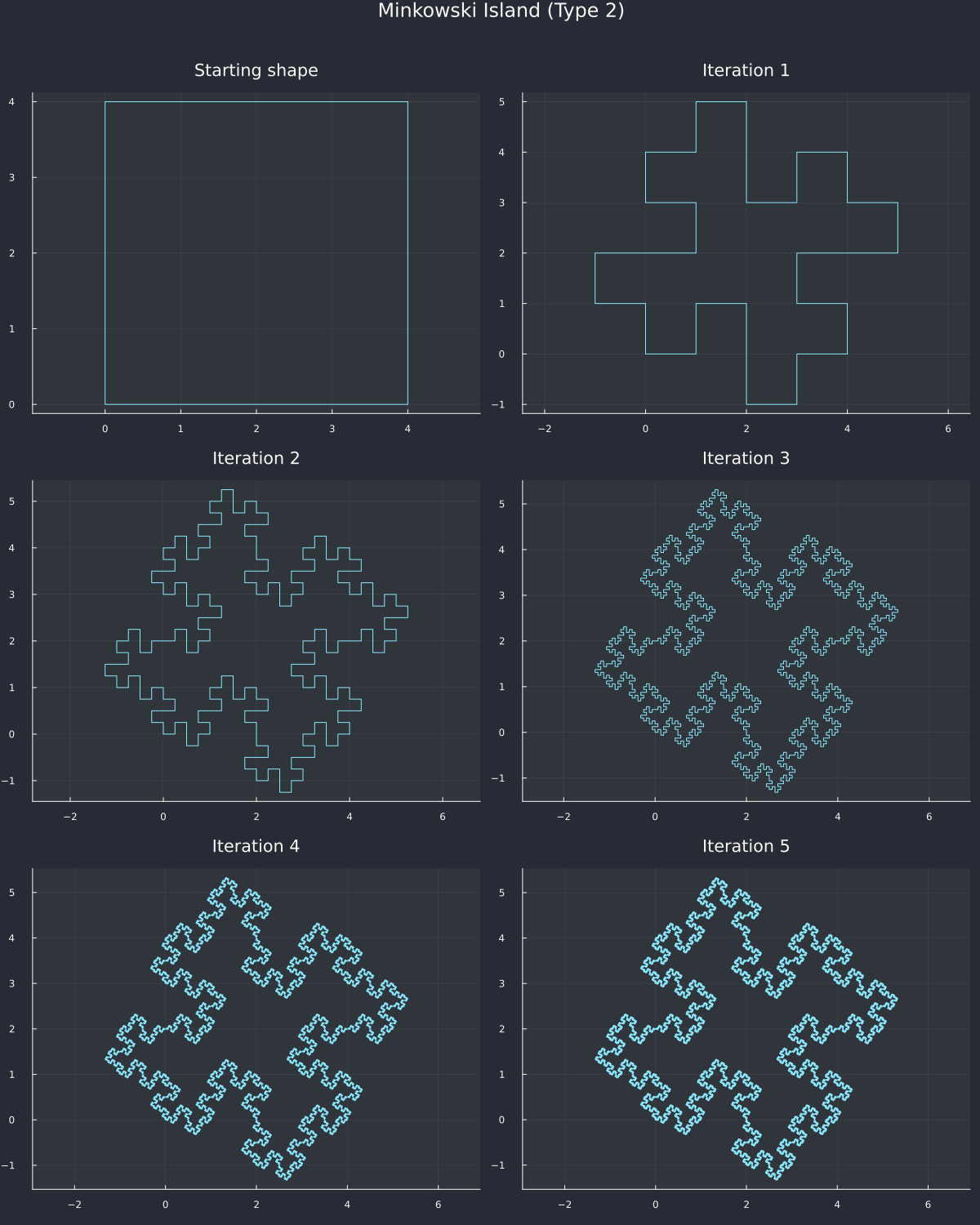
Or even starting from a diamond shape

We can even modify the original production rule to a simpler "→ becomes →↺→↻→↻→↺→" to make a type 1 Minkowski curve

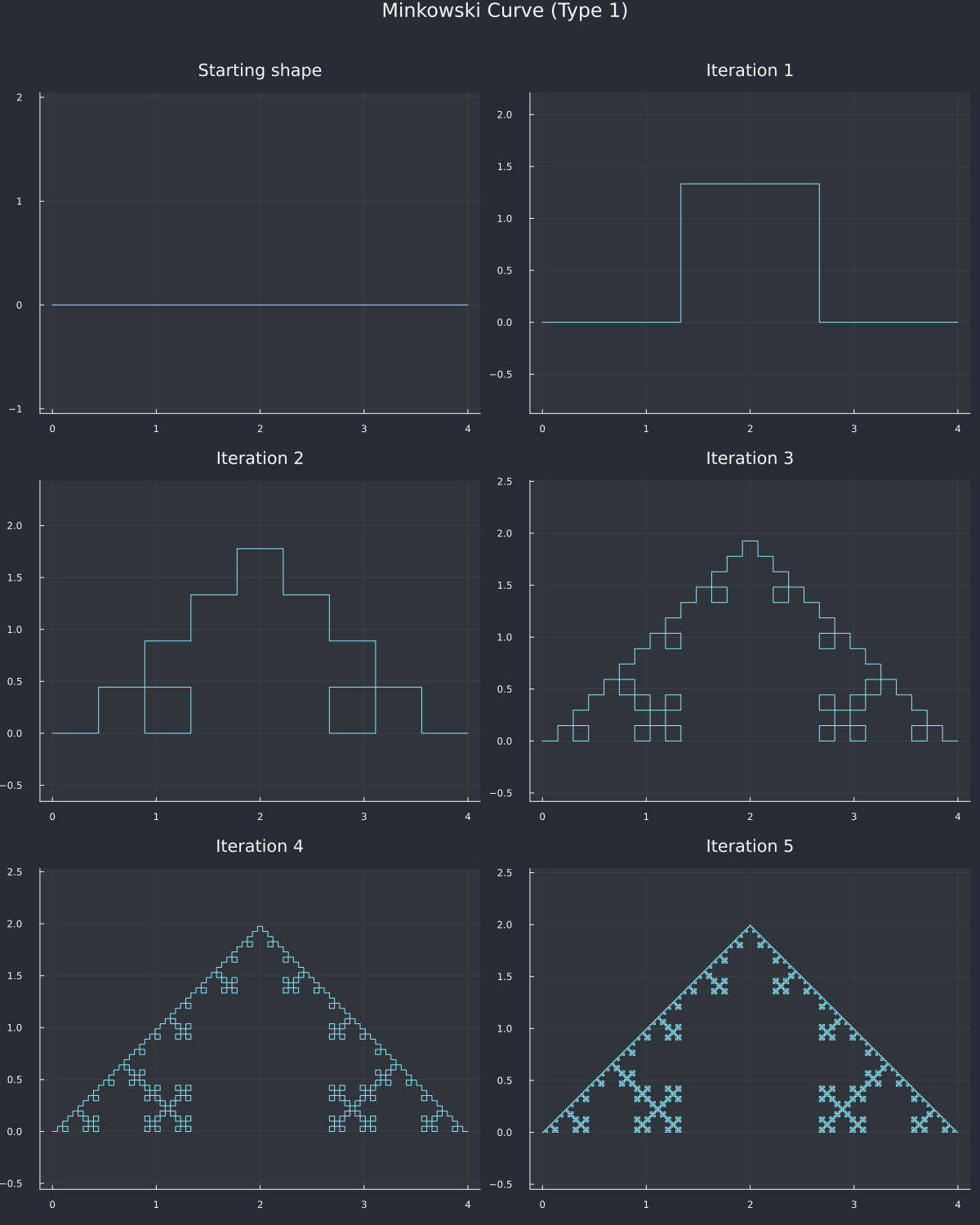
Hey, you can make this in Minecraft! I wonder how fractals could be used in procedural generation... oh well, that's a project for another day. Anyway, what I was saying is that if you start from a box, you can get this fun shape that can be used to make a fractal antenna:

Apparently, antennas with fractal designs are actually very efficient at operating in many different frequencies, as opposed to standard non-fractal antennas, which only operate well in a limited frequency range. Who knew?

If you instead start from a diamond, you can get this instead:

Conclusion

There's a million other fractals that can be made and infinite variations of the ones we've already seen. Alas, my time is limited and interests fleeting and varied, so I'm going to end this off here before I get too carried away. Still, there's tons to do here, both in pure fractals (more line fractals, 2D fractals, stochastic generations, other means of generation...) and in practical applications (the aforementioned procedural generation, fractal data compression, fractal art, wave dampening), so there's a good chance I'll be back on this eventually. Until then, I'll leave this off with a fancy fractal I invented by creating a somewhat ridiculous production rule: → becomes →↻→↻→↺→↺→↻→→↺→→↺→↻→→↻→↻→↺→↻→↺→↺→↻→↺→↺→→↻→↺→→↻→↺→→↻→↻→↺→↻→↻→↺→↻→↺→↺→→↺→↻→↻→→↻→→↺→↻→↻→↺→↺→.